La Retta: Equazione e Coefficiente Angolare - Guida Completa con Esercizi Risolti
1) Introduzione
2) L'Equazione della Retta: Forma Generale e Forma Esplicita
3) Il Coefficiente Angolare: Cosa Significa?
4) Rette Parallele e Perpendicolari
4) Esercizi Pratici
5) Applicazioni Pratiche della Geometria Analitica
6) Conclusioni
Introduzione
La retta è un concetto fondamentale in geometria analitica e rappresenta la base di molte applicazioni in matematica, fisica e ingegneria.
In questo articolo, esploreremo l'equazione della retta e il suo coefficiente angolare, partendo dalle basi fino a concetti più avanzati. Il tutto sarà accompagnato da esercizi risolti per tutti i livelli.
L'Equazione della Retta: Forma Generale e Forma Esplicita
L'equazione di una retta nel piano cartesiano può essere scritta in diversi modi. I più utilizzati sono:
Forma implicita
Ax + By + C = 0
Dove:
A, B e C sono coefficienti reali,
A e B non possono essere entrambi uguali a zero.
Forma esplicita
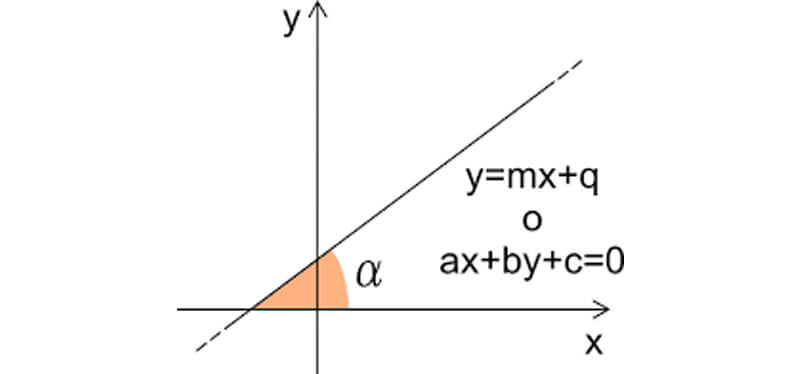
y = mx + q
Dove:
m è il coefficiente angolare, che rappresenta l'inclinazione della retta,
q è l'intercetta con l'asse y, ovvero il punto in cui la retta interseca l'asse delle ordinate (x = 0).
Il Coefficiente Angolare: Cosa Significa?
Il coefficiente angolare m indica l'inclinazione della retta rispetto all'asse x.
Se m > 0, la retta è crescente (sale da sinistra a destra).
Se m < 0, la retta è decrescente (scende da sinistra a destra).
Se m = 0, la retta è orizzontale.
Se la retta è verticale, il coefficiente angolare non è definito.
Il coefficiente angolare si calcola come:
m = (y2 - y1) / (x2 - x1)
Questa formula misura la variazione di y rispetto a quella di x tra due punti P1(x1, y1) e P2(x2, y2) della retta.
Rette Parallele e Perpendicolari
Rette Parallele
Due rette sono parallele se hanno lo stesso coefficiente angolare:
m1 = m2 Ad esempio, le rette y = 3x + 2 e y = 3x − 5 sono parallele perché hanno m = 3.
Rette Perpendicolari
Due rette sono perpendicolari se il prodotto dei loro coefficienti angolari è uguale a -1:
m1 · m2 = −1
Esempio:
Se una retta ha m = 2, allora una retta perpendicolare deve avere m = − 1 / 2, perché:
2 x (− 1 / 2) = −1
Esercizi Pratici
Esercizio 1: Determinare l'Equazione della Retta (Base)
Problema:
Trova l'equazione della retta passante per il punto P(2, 3) e con coefficiente angolare m = 4.
Svolgimento:
Usiamo la formula della retta con il coefficiente angolare noto:
y − y1 = m(x − x1)
Sostituendo i valori dati:
y − 3 = 4(x − 2)
y − 3 = 4x − 8
y = 4x − 5
L'equazione della retta è y = 4x − 5.
Esercizio 2: Calcolo del Coefficiente Angolare (Intermedio)
Problema:
Trova il coefficiente angolare della retta passante per i punti A(1, 2) e B(4, 8).
Svolgimento:
Usiamo la formula del coefficiente angolare:
m = (y2 - y1) / (x2 - x1)
m = (8 - 2) / (4 − 1) = 6 / 3 = 2
Il coefficiente angolare della retta è 2.
Esercizio 3: Intersezione tra Due Rette (Avanzato)
Problema:
Trova il punto di intersezione tra le rette:
y = 2x + 3
y = −x + 5
Svolgimento:
Uguagliamo le due equazioni:
2x + 3 = −x + 5
Risolviamo per x:
2x + x = 5 − 3
3x = 2 => x = 2 / 3
Sostituiamo x = 2 / 3 in una delle equazioni, ad esempio y = 2x + 3:
y = 2(2 / 3) + 3 = 4 / 3 + 3 = 13 / 3
Il punto di intersezione è (2 / 3, 13 / 3)
Applicazioni Pratiche della Geometria Analitica
La retta e il coefficiente angolare trovano applicazione in diversi ambiti:
✅ Fisica: traiettorie di oggetti in moto, ottica geometrica
✅ Ingegneria: piani inclinati, strutture edili
✅ Economia: modelli di crescita lineare
Conclusioni
Abbiamo esplorato tutto sulla retta: equazione, coefficiente angolare, rette parallele e perpendicolari. Ora sei pronto a risolvere esercizi più complessi!
Fonti: libri scolastici superiori

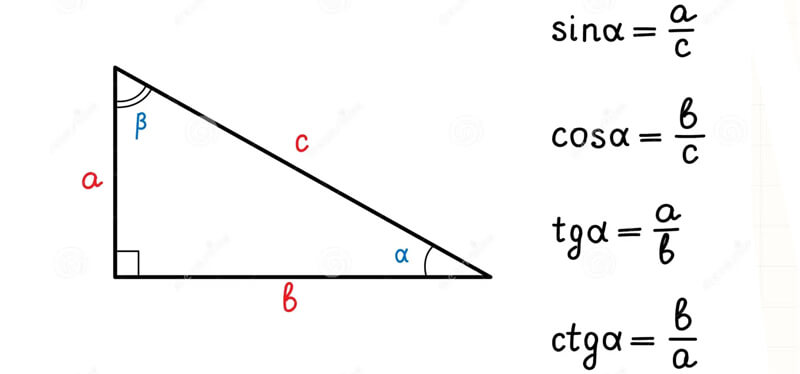 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
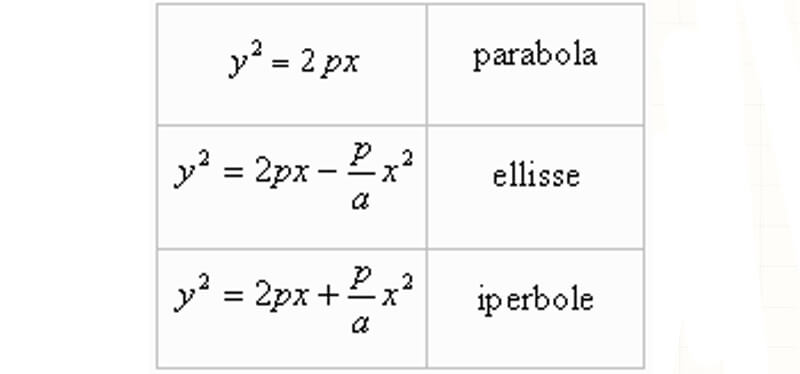 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
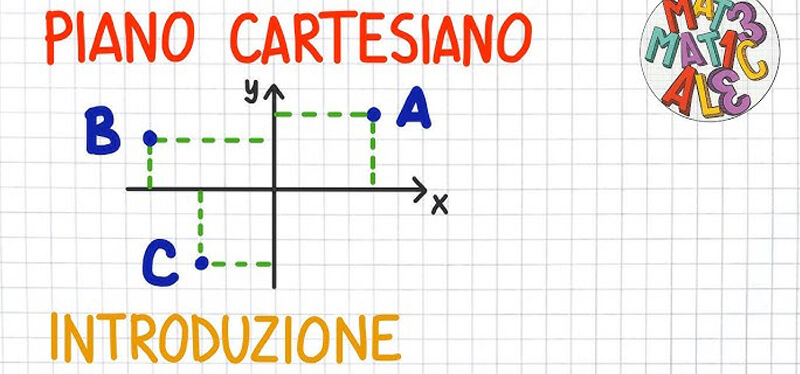 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
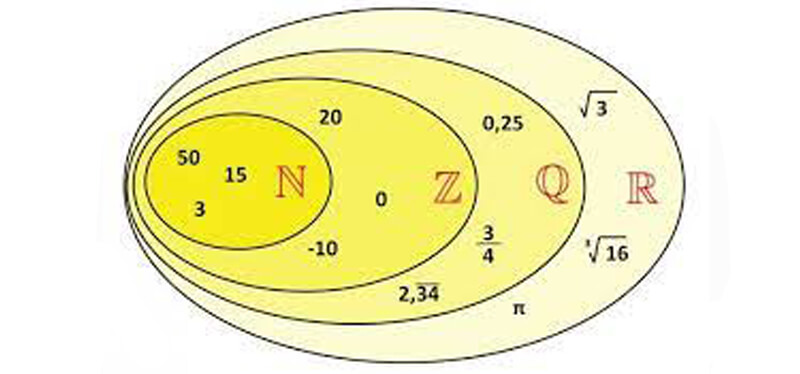 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici