Guida Completa alle Equazioni di Secondo Grado: Teoria, Esercizi e Approfondimenti

1) Introduzione
2) Cos'è un'Equazione di Secondo Grado?
3) Risoluzione delle Equazioni di Secondo Grado
4) Esercizi Pratici: Dalle Basi agli Approfondimenti
5) Applicazioni delle Equazioni di Secondo Grado
6) Conclusioni
Introduzione
Le equazioni di secondo grado sono un argomento fondamentale dell'algebra e trovano applicazione in fisica, economia, ingegneria e molte altre discipline. Questo articolo è pensato per chi parte da zero e per chi vuole approfondire il tema con esercizi avanzati e curiosità matematiche
Cos'è un'Equazione di Secondo Grado?
Un'equazione di secondo grado è un'equazione della forma: ax2 + bx + c = 0 dove:
a,b,c sono numeri reali con a ≠ 0
x è l'incognita da trovare.
Esempi di Equazioni di Secondo Grado
x2 −5x + 6 = 0 (equazione completa)
x2 −9 = 0 (equazione senza termine di primo grado)
x2 +4x = 0 (equazione senza termine noto)
Risoluzione delle Equazioni di Secondo Grado
Metodo 1: Formula Risolutiva (o Formula di Bhaskara)
L'equazione completa ax2 + bx + c = 0 si risolve con la formula del delta:
x = (-b ± √b2 -4ac) / 2a
Dove: Δ = b2 −4ac è il discriminante, che determina il numero e la natura delle soluzioni.
Analisi del Discriminante
Se Δ > 0 -> due soluzioni reali e distinte.
Se Δ = 0 -> una soluzione reale doppia.
Se Δ < 0 -> due soluzioni complesse coniugate.
Metodo 2: Scomposizione in Fattori
Se l'equazione è facilmente scomponibile, possiamo risolverla senza la formula del delta.
Esempio:
x2 −5x + 6 = 0
Possiamo scomporre come:
(x−3)(x−2) = 0
Da qui otteniamo x − 3 = 0 oppure x − 2 = 0,
quindi x1 = 3 e x2 = 2.
Metodo 3: Completamento del Quadrato
Risolvi x2 +6x + 5 = 0 completando il quadrato.
x2 +6x = −5
Aggiungiamo (6/2)2 = 9 a entrambi i membri:
x2 +6x + 9 = 4
Ora possiamo scrivere:
(x + 3)2 = 4
Prendiamo la radice quadrata:
x + 3 = ± 2
x = −3 ± 2
Risultati:
x1 = −1, x2 = −5
Esercizi Pratici: Dalle Basi agli Approfondimenti
Esercizio 1: Risoluzione con la Formula del Delta
Problema:
Trova le soluzioni di: x2 −5x + 6 = 0
Svolgimento:
Calcoliamo il discriminante:
Δ = (-5)2 −4(1)(6) = 25 - 24 = 1
Poiché Δ > 0, ci sono due soluzioni reali e distinte:
x = (-(-5) ± √1) / 2(1) = (5 ± 1) / 2
x1 = (5 + 1) / 2 = 6/2 / 3
x2 = (5 - 1) / 2 = 4/2 = 2
Risultato:
x1 = 3, x2 = 2.
Esercizio 2: Equazione con Delta Zero
Problema:
Trova le soluzioni di: x2 −4x + 4 = 0
Svolgimento:
Δ = (−4)2 −4(1)(4) = 16 − 16 = 0
Poiché Δ = 0, l'equazione ha una soluzione doppia:
x = (-(-4) ± √0) / 2(1) = 4/2 = 2
Risultato:
x = 2 (soluzione doppia).
Esercizio 3: Equazione con Soluzioni Complesse
Problema:
Trova le soluzioni di: x2 + x + 1 = 0
Svolgimento:
Δ = (1)2 −4(1)(1) = 1 − 4 = −3
Poiché Δ < 0, le soluzioni sono complesse:
x = (-1 ± √-3) / 2(1) = (-1 ± i√3) / 2
Risultato:
x1 = (-1 + i√3) / 2, x2 = (-1 - i√3) / 2
Applicazioni delle Equazioni di Secondo Grado
Fisica: Moto di un Proiettile
Un oggetto lanciato verticalmente segue l'equazione:
h = h0 + v0t - 1/2gt2
Che è un'equazione di secondo grado nel tempo t.
Finanza: Modelli di Crescita e Decadimento
Le equazioni quadratiche appaiono in modelli economici che descrivono la crescita o la perdita di valore di investimenti.
Conclusioni
Le equazioni di secondo grado sono ovunque, dalla matematica pura alle applicazioni reali. Ora sai come risolverle con metodi diversi, interpretare il discriminante e applicarle a contesti pratici.
Continua ad allenarti con nuovi esercizi e diventa un vero esperto di equazioni quadratiche! 🎯
Fonti: libri scolastici superiori

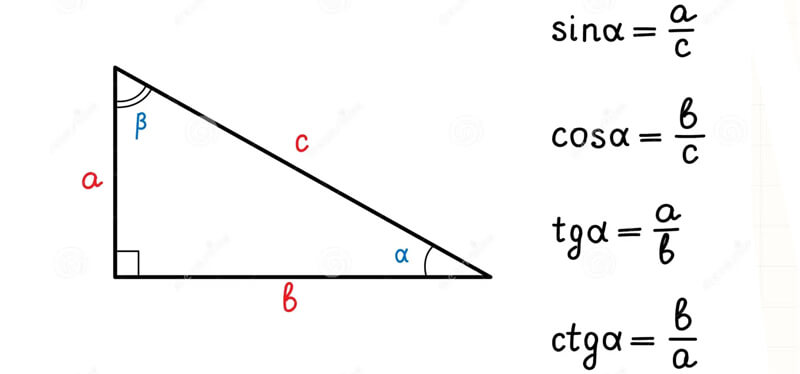 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
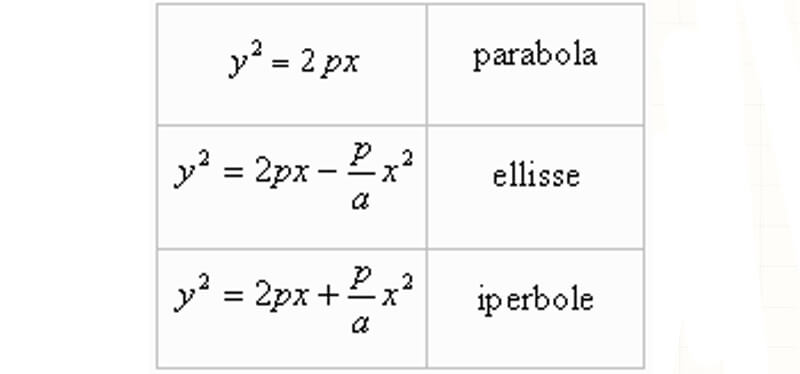 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
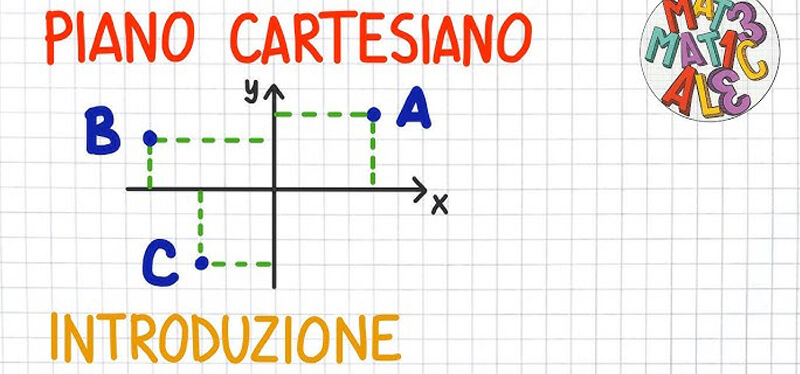 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
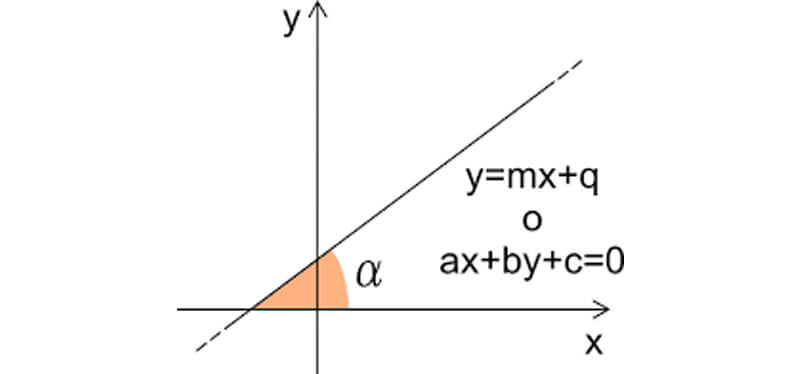 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici