Alla Scoperta delle Equazioni di Primo Grado: Teoria ed Esercizi

1) Introduzione
2) Video Riassuntivo
3) Introduzione alle Equazioni di Primo Grado
4) Concetti Fondamentali e Dimostrazione Intuitiva
5) Esercizi Pratici: Dalle Basi agli Approfondimenti
6) Approfondimenti e Curiosità
7) Conclusioni
Introduzione
Le equazioni di primo grado sono uno degli argomenti fondamentali in algebra, rappresentando il primo approccio concreto alla risoluzione di problemi matematici. Questo articolo è pensato per guidare il lettore, sia che si stia avvicinando per la prima volta a questo concetto, sia che si desideri rinfrescare le proprie competenze con esempi ed esercizi stimolanti.
Video Riassuntivo
Introduzione alle Equazioni di Primo Grado
Un'equazione di primo grado è un'equazione in cui la variabile compare elevata alla prima potenza. La forma generale è: ax + b = 0
dove:
a e b sono numeri reali;
a ≠ 0, altrimenti l'equazione non sarebbe di primo grado;
x è l'incognita da determinare.
La soluzione dell'equazione si ottiene isolando x, arrivando alla formula: x = − a/b.
Questa formula rappresenta il fulcro del metodo risolutivo per le equazioni di primo grado, ma è solo l'inizio di un percorso che esploreremo insieme.
Concetti Fondamentali e Dimostrazione Intuitiva
Cosa Significa "Risolvere" un'Equazione?
Risolvere un'equazione vuol dire trovare il valore (o i valori) della variabile che, sostituiti nell'equazione, rendono vera l'uguaglianza. Per un'equazione lineare, essendo di primo grado, esiste una sola soluzione.
Perché Funziona la Soluzione x = − a/b?
Immagina di voler "annullare" il termine costante b. Per fare questo, aggiungi −b ad entrambi i lati:
ax = −b
Successivamente, dividendo entrambi i lati per a (ricordando che a non è zero), ottieni la soluzione:
x = − a/b
Questo procedimento evidenzia il principio di equilibrio nelle equazioni: ciò che si fa da una parte dell'uguale va fatto anche dall'altra.
Esercizi Pratici: Dalle Basi agli Approfondimenti
Esercizio 1: Semplice Esercizio per Principianti
Problema:
Risolvi l'equazione: 3x + 6 = 0
Svolgimento:
1) Sottrai 6 da entrambi i lati: 3x = −6
2) Dividi per 3: x = −2
Risultato:
x = −2
Esercizio 2: Esercizio con Coefficienti Negativi
Problema:
Risolvi l'equazione: −5x +15 = 0
Svolgimento:
1) Sottrai 15 da entrambi i lati: −5x = −15
2) Dividi per -5: x = 3
Risultato:
x = 3
Esercizio 3: Esercizio con Parametri
Problema:
Considera l'equazione: ax + b = 0, dove a e b sono parametri. Esprimi x in funzione di a e b e discuti il caso in cui a = 0.
Svolgimento:
- Se a ≠ 0, la soluzione è: x = − a/b
- Se a = 0, l'equazione diventa: b = 0.
In questo caso:
Se anche b = 0, l'equazione è un'identità (vero per ogni x).
Se b ≠ 0, l'equazione è impossibile (non esistono soluzioni).
Risultato:
La soluzione generale è x = − a/b per a ≠ 0, con le eccezioni specificate per a = 0.
Esercizio 4: Problema Avanzato per Esperti
Problema:
Risolvi il sistema di equazioni (entrambe dentro la stessa {):
{ 2x −3y +5 = 0
{ 4x +y −7 = 0
Svolgimento:
1) Dalla seconda equazione, isoliamo y: y = 7 −4x
2) Sostituiamo y nella prima equazione: 2x −3(7 −4x) +5 = 0
3) Svolgiamo i calcoli: 2x −21 +12x +5 = 0 ⇒ 14x −16 = 0
4) Risolviamo per 14x = 16 ⇒ x = 16/14 = 8/7
5) Calcoliamo y: y = 7 −4(8/7) = 7 − 32/7 = (49−32)/7 = 17/7
Risultato:
x = 8/7 e y = 17/7
Approfondimenti e Curiosità
Applicazioni delle Equazioni di Primo Grado
Problemi della vita reale: Le equazioni di primo grado sono utilizzate per risolvere problemi economici, calcolare budget, risolvere questioni di proporzioni e tanti altri contesti quotidiani.
Fisica e ingegneria: Utili per modellare fenomeni lineari, come il moto rettilineo uniforme o per risolvere circuiti elettrici.
Curiosità per gli Appassionati
Storia: Le equazioni lineari sono state studiate già nelle antiche civiltà, ed il metodo per risolverle ha subito evoluzioni fino ad arrivare alle tecniche moderne.
Generalizzazioni: L'approccio usato per le equazioni di primo grado è alla base di tecniche risolutive in algebra lineare, un argomento che apre le porte allo studio degli spazi vettoriali e delle trasformazioni lineari.
Conclusioni
Le equazioni di primo grado rappresentano un punto di partenza essenziale per chiunque desideri avvicinarsi al mondo della matematica. La loro semplicità, unita alla capacità di modellare numerosi problemi reali, le rende uno strumento indispensabile tanto per i neofiti quanto per gli esperti.
Speriamo che questo articolo, con la sua panoramica teorica e i numerosi esercizi, abbia suscitato il tuo interesse e ti abbia offerto gli strumenti necessari per approfondire ulteriormente l'argomento. La chiave per padroneggiare la matematica è l'esercizio costante e la curiosità di scoprire nuove connessioni.
Buono studio e continua a sfidare te stesso con nuovi problemi!
Fonti: libri scolastici superiori

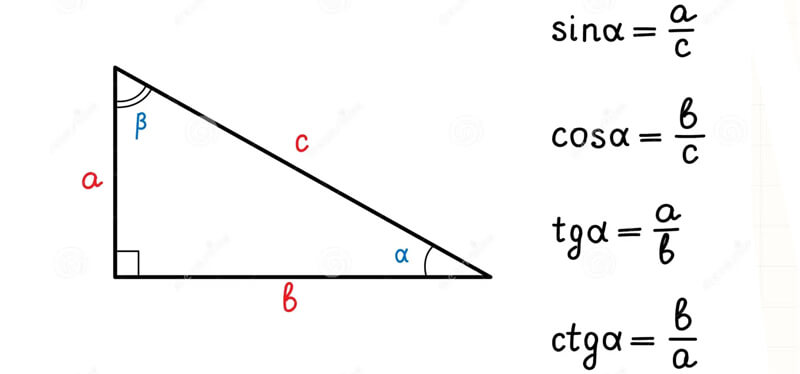 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
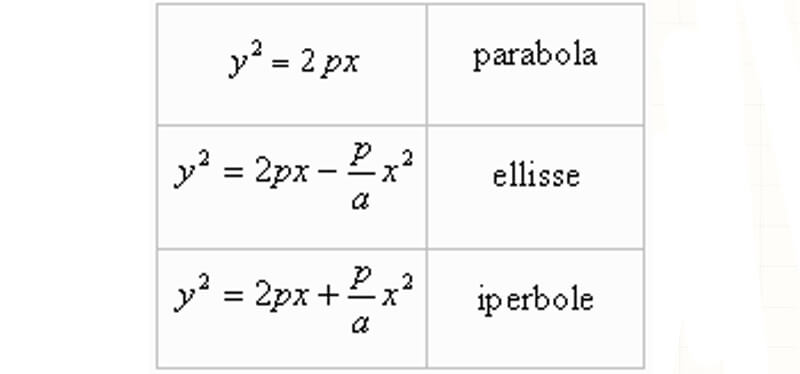 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
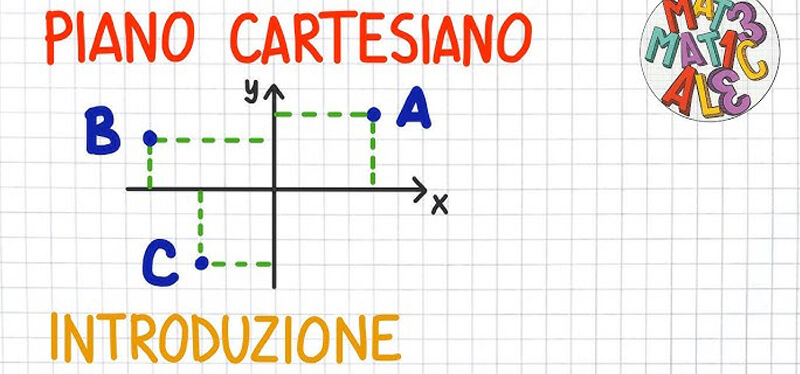 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
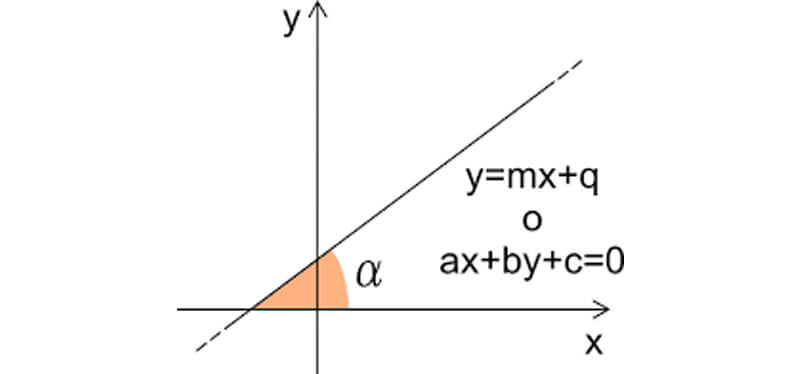 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
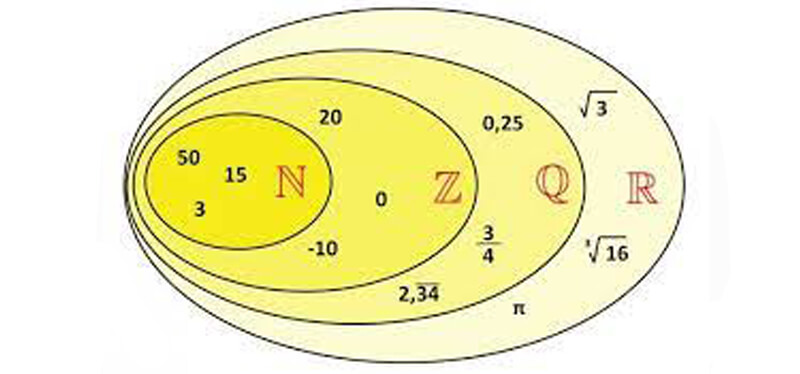 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici