Guida Completa al Calcolo delle Probabilità: Teoria, Esercizi e Approfondimenti

1) Introduzione
2) Cos'è la Probabilità?
3) Regole Fondamentali della Probabilità
4) Esercizi Pratici: Dalle Basi agli Approfondimenti
5) Curiosità e Applicazioni
6) Conclusioni
Introduzione
Il calcolo delle probabilità è un ramo fondamentale della matematica che trova applicazioni in numerosi campi, dalla statistica alla finanza, dalla fisica all'intelligenza artificiale.
Cos'è la Probabilità?
La probabilità misura il grado di incertezza di un evento e si esprime con un numero compreso tra 0 e 1:
P = 0 significa che l'evento è impossibile.
P = 1 significa che l'evento è certo.
Se 0 < P < 1, l'evento ha una certa possibilità di verificarsi.
Esempio Intuitivo
Immagina di lanciare una moneta:
La probabilità che esca testa è P(T) = 1/2
La probabilità che esca croce è P(C) = 1/2
Il calcolo della probabilità si basa su esperimenti casuali, cioè situazioni in cui non possiamo prevedere con certezza il risultato.
Regole Fondamentali della Probabilità
Definizione Classica di Probabilità:
Se un esperimento ha n esiti ugualmente probabili e un evento favorevole può realizzarsi in k di essi, allora la probabilità dell'evento è: P(A) = k/n
Esempio:
Lanciando un dado a sei facce, la probabilità di ottenere un numero pari (2, 4 o 6) è:
P(numero pari) = 3/6 = 1/2
Proprietà Fondamentali
1) Probabilità dell'evento complementare:
P(Ac) = 1 − P(A)
Se la probabilità di pioggia domani è 0.3, allora la probabilità che non piova è 1 − 0.3 = 0.7
2) Somma delle probabilità di eventi incompatibili:
Se due eventi A e B sono mutuamente esclusivi (cioè non possono verificarsi insieme), allora:
P(A o B) = P(A) + P(B)
Esempio:
La probabilità di estrarre un asso o un re da un mazzo di 52 carte è:
P(asso) + P(re) = 4/52 + 4/52 = 8/52 = 2/13
3) Probabilità Condizionata:
La probabilità di un evento A sapendo che B è già accaduto si calcola con:
P(A | B) = P(A ∩ B) / P(B)
Esempio:
In una classe di 10 studenti, 6 sono femmine. Se sappiamo che uno studente scelto a caso è alto più di 1,70 m e tra questi solo 3 sono femmine, la probabilità di aver scelto una femmina dato che è alta più di 1,70 m è:
P(F | H) = P(F ∩ H) / P(H) = (3/10) / (5/10) = 3/5 = 0.6
Esercizi Pratici: Dalle Basi agli Approfondimenti
Esercizio 1: Lancio di un Dado
Problema:
Qual è la probabilità di ottenere un numero maggiore di 4 lanciando un dado a sei facce?
Svolgimento:
Gli esiti favorevoli sono {5, 6}. Il numero totale di esiti possibili è 6, quindi:
P(numero > 4) = 2/6 = 1/3
Esercizio 2: Estrazione di Carte
Problema:
Qual è la probabilità di pescare un cuore da un mazzo di carte francesi da 52 carte?
Svolgimento:
Ci sono 13 cuori nel mazzo, quindi:
P(cuore) = 13/52 = 1/4
Esercizio 3: Probabilità Condizionata Avanzata
Problema:
Un'azienda ha il 70% di possibilità di ricevere un ordine se fa una buona offerta e il 40% se non la fa. Se l'azienda decide di fare una buona offerta nel 60% dei casi, qual è la probabilità che riceva l'ordine?
Svolgimento:
Usiamo il teorema delle probabilità totali:
P(O) = P(O | B)P(B) + P(O | N)P(N)
Dove:
P(O | B) = 0.7 (probabilità di ricevere l'ordine con una buona offerta).
P(B) = 0.6 (probabilità di fare una buona offerta).
P(O | N) = 0.4 (probabilità di ricevere l'ordine senza fare un'offerta).
P(N) = 0.4 (probabilità di non fare un'offerta).
Calcoliamo:
P(O) = (0.7 x 0.6) + (0.4 x 0.4) = 0.42 + 0.16 = 0.58
Quindi, la probabilità che l'azienda riceva l'ordine è 0.58 (58%).
Approfondimenti e Curiosità
Paradosso di Monty Hall
Uno dei problemi più famosi della probabilità è il paradosso di Monty Hall. Se partecipi a un quiz televisivo e ti vengono presentate tre porte, una con un'auto dietro e due con capre, e il conduttore ti fa cambiare porta dopo averne aperta una, conviene cambiare?
La risposta è sì! Cambiare porta aumenta la probabilità di vincere l'auto da 1/3 a 2/3.
Conclusioni
Il calcolo delle probabilità è uno strumento potentissimo che troviamo ovunque, dal gioco d'azzardo alla previsione meteo, fino all'intelligenza artificiale. Saperlo padroneggiare ti permette di affrontare situazioni incerte con una mentalità razionale e strategica.
Continua ad allenarti con esercizi sempre più complessi e scoprirai quanto la probabilità sia affascinante e utile! 🔢🎲
Fonti: libri scolastici superiori

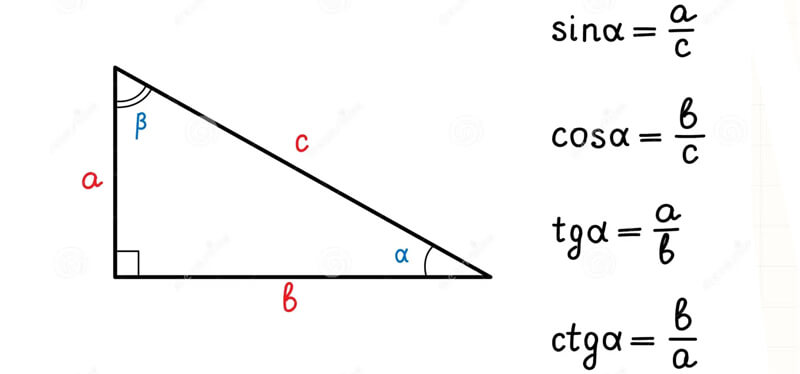 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
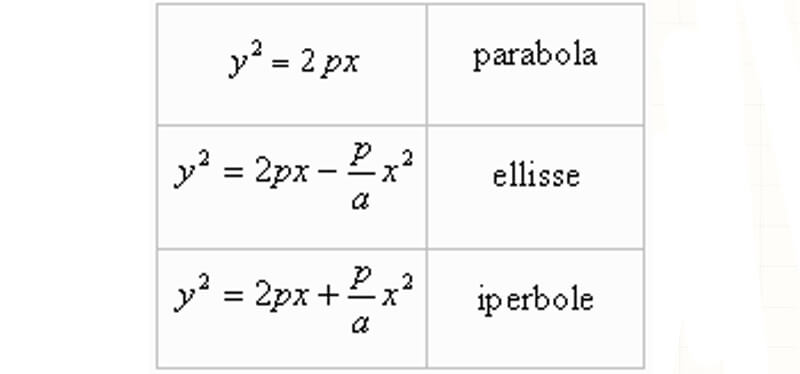 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
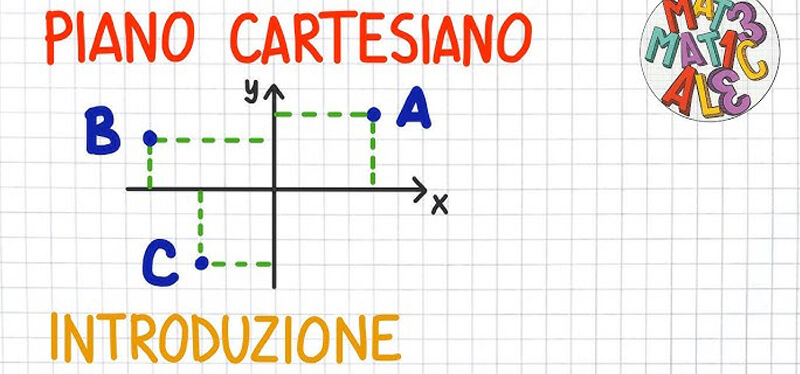 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
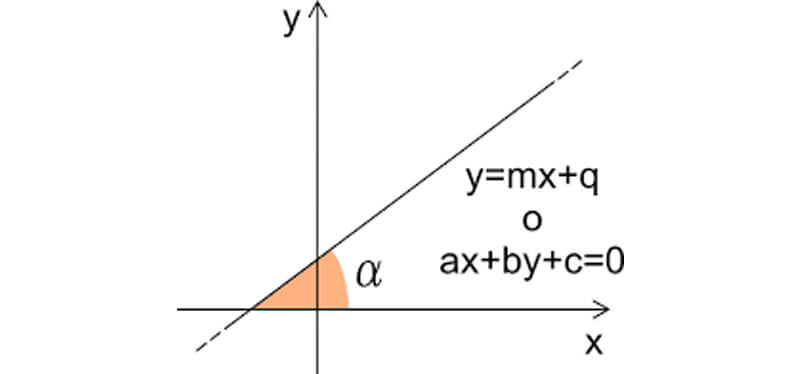 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
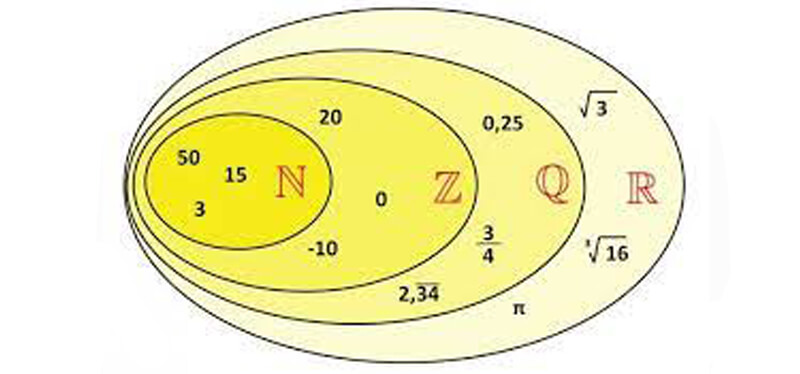 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici